TANGENTI GEOMETRICHE
Si possono dare varie definizioni intuitive di retta tangente a una curva nel piano.
La parola tangente viene da tangere cioè toccare. L'idea intuitiva di una retta tangente a una curva è quella di una retta che "tocca" la curva senza "tagliarla" o "secarla" (immaginando la curva come se fosse un oggetto fisico non penetrabile). Una retta che attraversa la curva "tagliandola" è invece chiamata secante.
Data inoltre una secante che passa per due punti distinti P e Q di una curva, si può pensare la tangente in P come la retta cui tende (eventualmente) la secante quando il punto Q si avvicina a P lungo la curva.
Nell'ambito della geometria sintetica si possono dare definizioni rigorose alternative di retta tangente a curve specifiche che funzionano solo per tali curve. Ad esempio la tangente ad una circonferenza di centro O e raggio r in un suo punto P può essere definita come la retta passante per P e avente distanza r da O, o come l'unica retta del piano avente in comune con la circonferenza il solo punto P.
In una geometria a più dimensioni, si può definire il piano tangente ad una superficie in modo simile e, generalizzando, lo spazio tangente.
Circonferenze tangenti esternamente 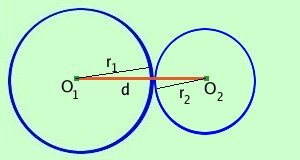
O1 O2____ = r1 + r2 d = r1+ r2
Le circonferenze sono fra loro tangenti esternamente se la distanza d fra i due centri e' uguale al valore della somma dei due raggi
Viceversa: se la distanza fra i due centri e' uguale al valore della somma dei due raggi allora le circonferenze sono tangenti esternamente fra loro
TAVOLA 6-TANGENTI
1. Disegnare la tangente ad una circonferenza per il suo punto P. Raggio circonf. r=35
2. Disegnare la circonf. tangente ad una retta passante per un punto A esterno e per un punto P sulla retta.
3. Disegnare una circonf. tangente ad una circonf. (r=32) nel suo punto P e passante per un punto A esterno ad essa.
4. Disegnare le rette tangenti ad una circonf. (r=38) e passanti per un punto P esterno ad essa.
5. Disegnare le tangenti esterne a due circonferenze di raggio diverso. r=30; r’=18
6. Disegnare le tangenti interne a due circonferenze di raggio diverso. r=30; r’=18
Es.1 Tav.6
1. Costruire una circonferenza di r=35 (Di segno evidente).
2. Scegliere un punto P a piacere su di essa.
3. Collegare O, centro della circonferenza,con il punto P, e prolungare verso l’esterno.
4. Costruire la perpendicolare della semiretta OP , passante per il punto P.
5. Questa perpendicolare è la tangente cercata che va tracciata in segno evidente continuo.
Es.2 Tav.6
1. Disegnare una retta generica e stabilire su di essa il punto P e il punto A esterno.
2. Collegare il punto A con il punto P e costruire l’asse del segmento AP..
3. Costruire la perpendicolare alla retta passante per il punto P.
4. Perpendicolare e asse si intersecano nel punto O’.
5. O’ è il centro della circonf., di raggio O’-P ,tangente alla retta e passante per i punti A e P.
6. Evidenziare la circonf. e la retta iniziale.
Es.3 Tav.6
1. Disegnare una circonferenza di diametro 40 e centro O; fissare un punto P su di essa e un punto A esterno ad essa.
2. Collegare A con P e costruire l’asse di questo segmento.
3. Collegare il centro O della circonferenza con il punto P e prolungare fino ad incontrare l’asse del segmento P-A.
4. Questa intersezione è il punto O’, centro della circonferenza cercata, tangente alla prima.
5. Evidenziare entrambe le circonferenze.
Es.4 Tav.6
1. Disegnare una circonf. Di raggio 38 e fissare un punto P esterno.
2. Collegare P con il centro O della circonferenza.
3. Costruire l’asse del segmento OP, individuando così il punto M.
4. Con centro in M tracciare la circonferenza di raggio MO.
5. Questa circonf. interseca la prima nei punti 1 e 2.
6. Per P-1 e per P-2 passano le tangenti alla circonf. cercate. Evidenziarle come la circonf. di partenza.
Es.5 Tav.6
1. Disegnare le due circonf. di raggio r=30 e r’=18 e centri O e O’
2. Collegare i due centri e costruire l’asse del segmento O-O’ individuando così il punto M.
3. Portare con il compasso la dimensione del raggio più piccolo (18) a partire dal punto 1 (intersezione fra la congiungente O-O’ e la circonf. di centro O) ottenendo così il punto 2 sulla congiungente dei 2 centri (differenza di raggi).
4. Disegnare la circonferenza di centro O e raggio O-2.
5. Con centro in M e raggio M-O tracciare la circonferenza che taglia l’ultima circonferenza nei punti 3 e 4.
6. Collegare il punto O con il punto 4 e proseguire fino al punto 4’.
7. Collegare il punto O con il punto 3 e proseguire fino al punto 3’.
8. Tracciare le parallele alle semirette O-4’ e O-3’ a partire dal punto O’.
9. Queste intersecano la circonferenza di centro O’ nei punti 5 e 6.
10. Tracciare le rette passanti per i punti 4’-5 e per 3’-6, ottenendo così le tangenti cercate.
11. Evidenziare le prime due circonferenze tracciate e le tangenti.
Es.6 Tav.6
1. Disegnare le due circonf. di raggio r=30 e r’=18 e centri O e O’
2. Tracciare un raggio della circonf. di raggio 30 (O-1)e tracciare il raggio parallelo, ma in direzione opposta, della circonf. di raggio 18 (O’-2).
3. Collegare i punti 1 e 2 così trovati. e collegare anche i 2 centri O e O’ delle circonferenze.
4. Questi 2 collegamenti si intersecano nel punto I.
5. Costruire gli assi dei segmenti O-I e I-O’ individuando così i punti medi M e M’.
6. Disegnare le circonferenze di centri M e M’ e raggi M-O e M’-O’.
7. Queste due circonf, intersecano le due precedenti nei punti 3, e 4, 5 e 6.
8. Per i punti 5-I-4 e per i punti 3-I-6 passano le tangenti interne alle circonferenze.
9. Evidenziare le prime due circonferenze e le tangenti trovate.
MATERIALE PER IL DISEGNO
1) Album da disegno formato A3, fogli lisci, squadrati. Spessore a scelta.
2) Due matite di legno o portamine (contenitori di mine dotati di un pulsante che ne consente la fuoriuscita in base alle necessità) con mine HB ed F o, a scelta, 2H.
3) Temperamatite adeguato alla matita.
4) Compasso con vite di regolazione e con mina HB.
5) Gomma per matita.
6) Due squadrette (una con angoli 30°-60° e una con angoli da 45°).
7) Curvilinee (facoltativo).
8) Cerchiografo (facoltativo).
Secondo la normativa UNI 936/86 ( l’UNI, Ente Nazionale di Unificazione,in Italia, è l’organismo che dal 1921 coordina le regole per l’unificazione delle simbologie e delle normative per la rappresentazione tecnica) la dimensione dei fogli da disegno è:
Formato A4 mm 210x297
Formato A3 mm 297x420
Per tutti i formati deve essere previsto un margine tra i bordi esterni del formato finito e la squadratura che delimita la zona di esecuzione del disegno.
Durezza delle mine:
Tenerissime: 6B,5B,4B,3B (disegno a mano libera) del formato finito e la squadratura che delimita la zona di esecuzione del disegno.
Tenere: 2B (disegno a mano libera)
Semitenere: B, HB,F (disegno geometrico)
Medie: H (disegno geometrico e disegno tecnico)
Dure: dalla 2H alla 8H (disegno tecnico)
Durissime: 9H (usi particolari).

Per gli appunti, sia di disegno che di tecnologia, serve un quadernone a quadretti da 5mm.
Per trasportare più agevolmente tutto il necessario vi conviene utilizzare una cartella bianca larga almeno 50cm, così ci potete mettere sia l'album da disegno che le squadrette.
Non dimenticate di aver cura del vostro materiale.
Portatelo sempre con voi ad ogni lezione di disegno.
Con questo link si accede ad un altro sito per le classi prime Istituto Tecnico Industriale


